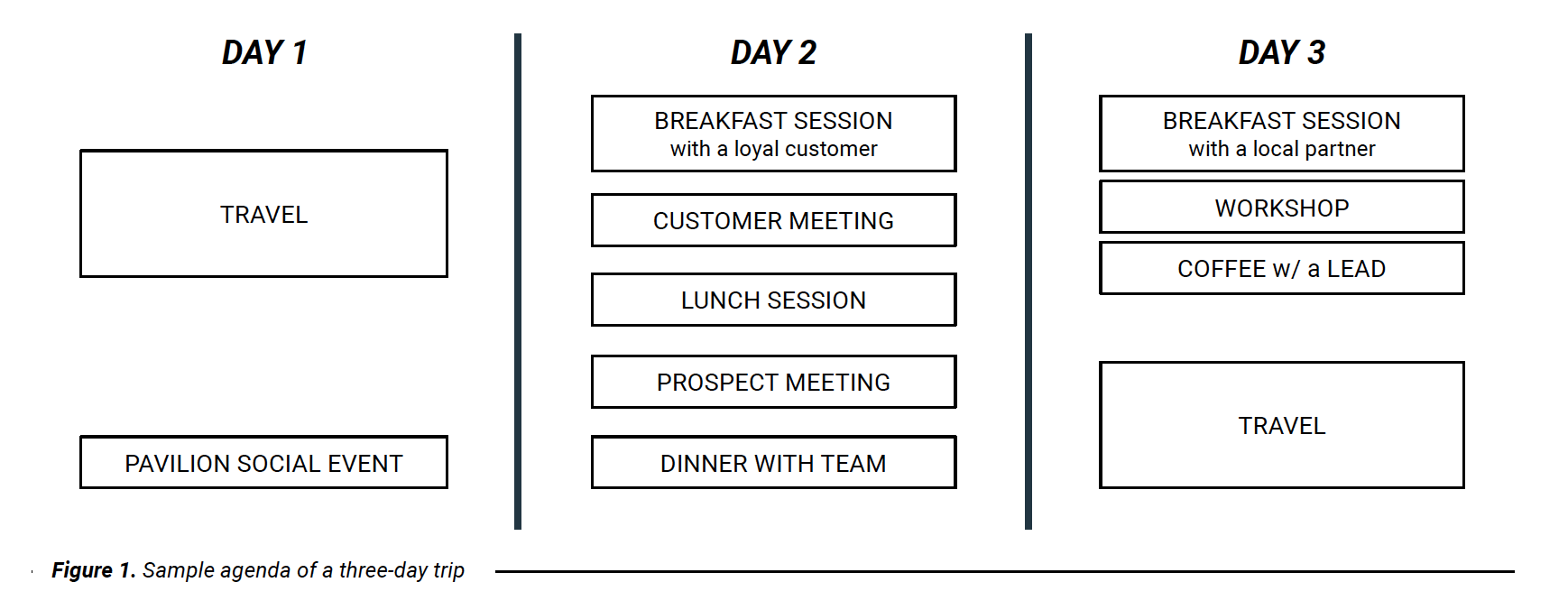
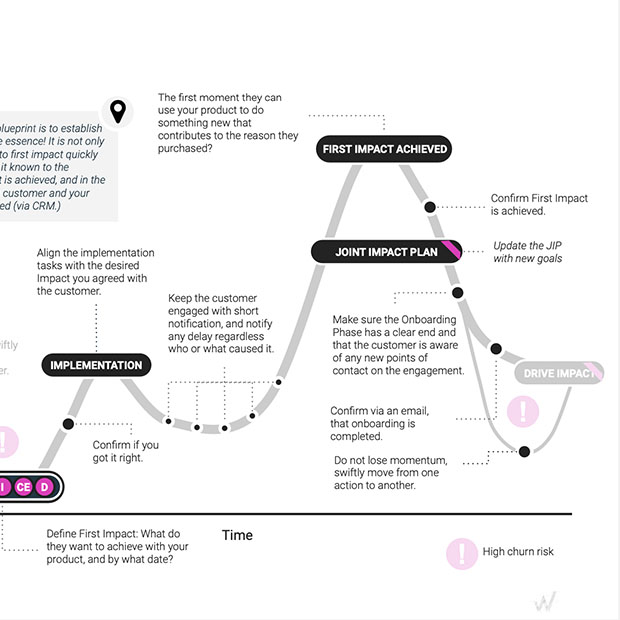
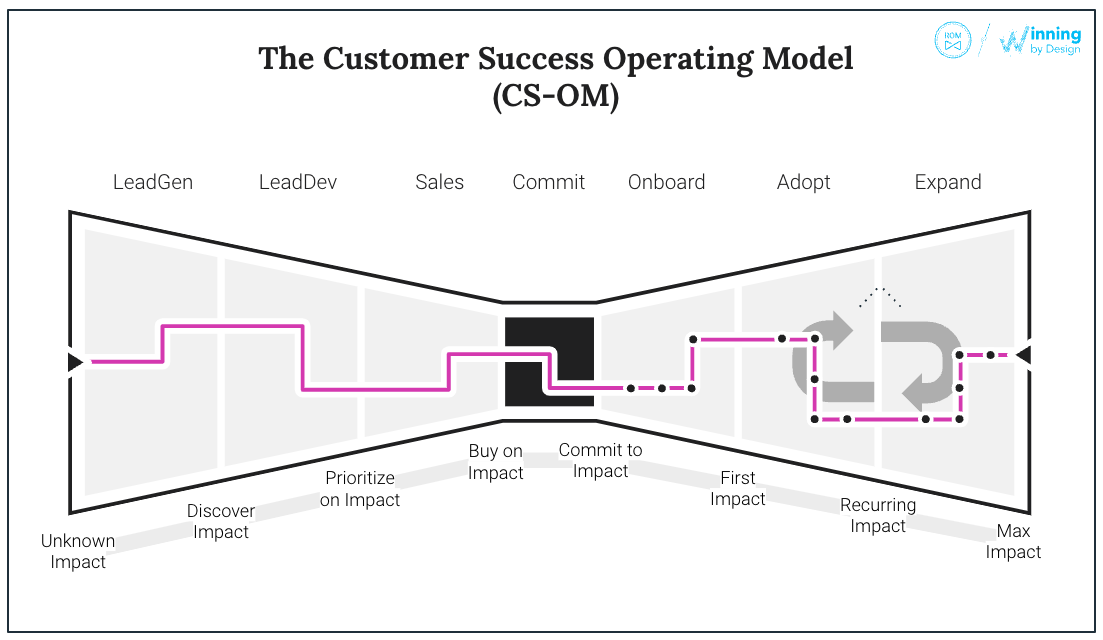
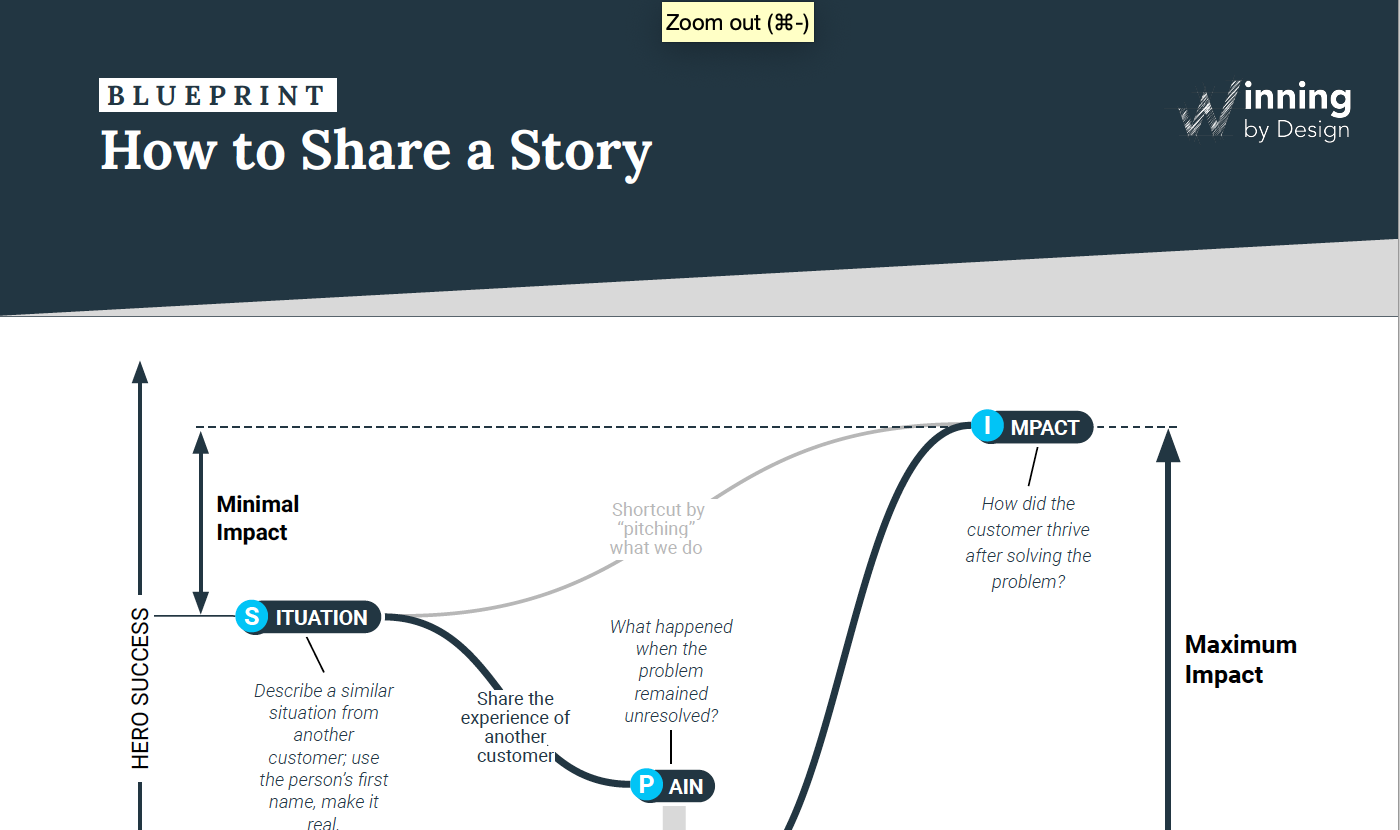
- Our Process
- Services
-
Training & Coaching
-
Prospecting for Impact
-
Prospecting into Enterprise Accounts
-
Selling for Impact
-
Selling into Enterprise Accounts
-
Customer Success for Impact
-
Account Management for Growth
-
Managing for Impact
-
Managing for Leadership
-
Revenue Architecture
-
Bowtie Analytics
-
Insight Engineering
-
 Skills Course: Discovery Using SPICED
Skills Course: Discovery Using SPICED -
 Skills Course: Storytelling
Skills Course: Storytelling -
 Facilitator Certification
Facilitator Certification
-
- Resources
- Clients
Resources